Journées MathSTIC Combinatoire & Probabilités 2024

3-4 oct. 2024 Villetaneuse (France)

Bienvenue !

Nous organisons deux journées de conférences les 3 et 4 octobre 2024 en combinatoire et probabilités.

Ces journées s'inscrivent dans le cadre de l'axe 3 (Physique mathématique, Physique Statistique, Combinatoire) de la fédération de recherche Math-STIC de l'Université Sorbonne Paris Nord, qui associe les laboratoires de mathématiques (LAGA), d'informatique (LIPN) et de traitement et transmission de l'information (L2TI).

Les exposés auront lieu dans l'amphi Euler de l'Institut Galilée.

Des repas (buffets) seront proposés le midi.

L'inscription est gratuite mais obligatoire pour faciliter l'organisation. Les inscriptions sont désormais closes.

Programme

Jeudi 3/10		Vendredi 4/10
9h30-10h	Café de bienvenue	9h-10h	Michael Drmota
10h-11h	Mireille Bousquet-Mélou	10h-10h30	Pause café
11h-12h	Mingkun Liu	10h30-11h30	Alice Contat
12h-14h	Pause déjeuner	11h30-12h30	Andrew Elvey Price
14h-15h	Armand Riera	12h30-14h	Pause déjeuner
15h-16h	Meltem Ünel	14h-15h	Enrica Duchi
16h-16h30	Pause café	15h-16h	Quentin Berger
16h30-17h30	Baptiste Louf

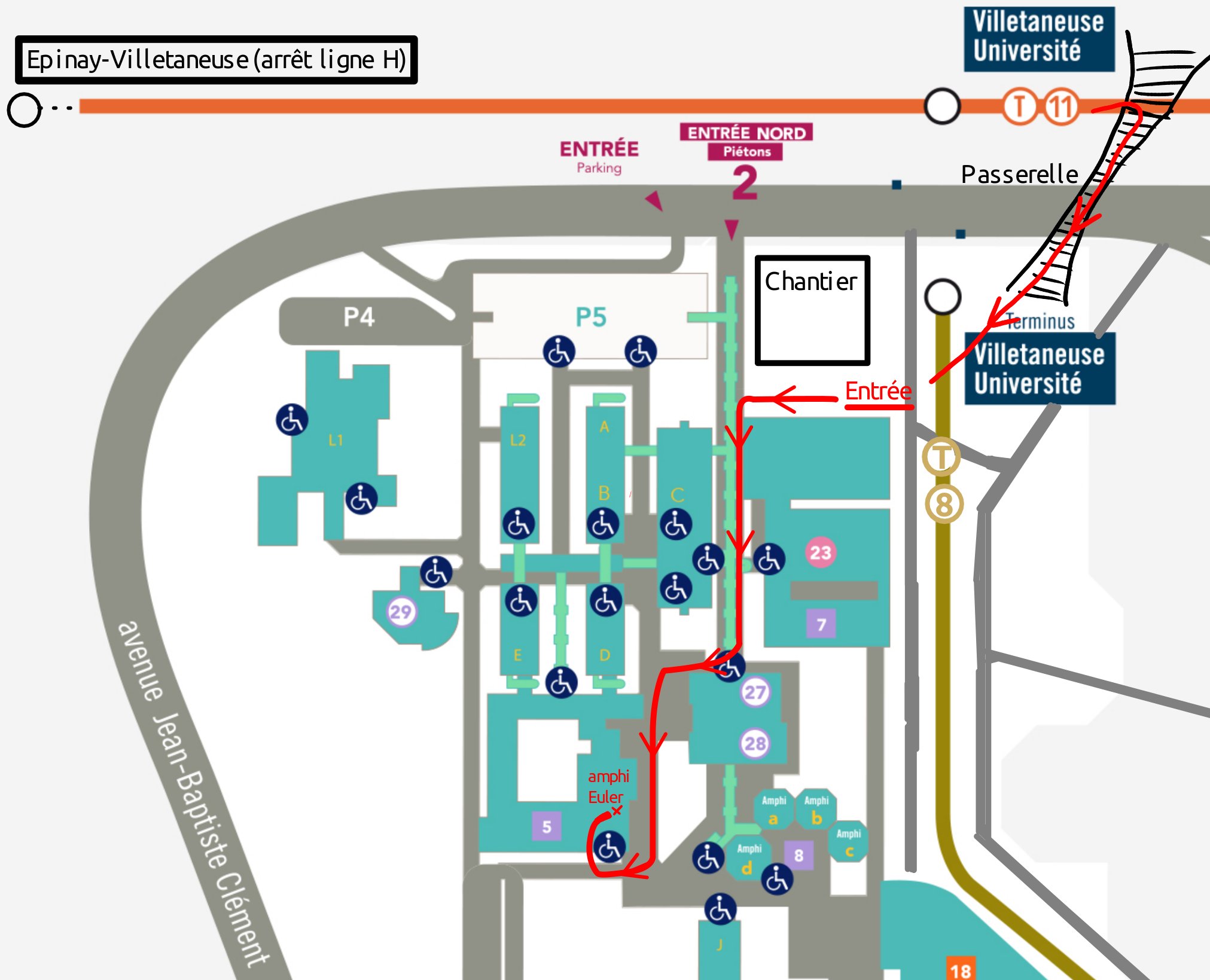
Jeudi 3/10

Mireille Bousquet-Mélou : Combinatorics of 3-coloured quadrangulations (slides)

This talk deals with the enumeration of (planar) maps equipped with a proper 3-colouring of their vertices. The case of triangulations is well-understood, with an algebraic generating function and bijective solutions. The case of general planar maps is still algebraic, but the combinatorial explanations for that are missing. We will focus on quadrangulations, for which algebraicity is lost.
We will see that this problem admits several interesting reformulations (in terms of orientations, of height functions...), which suggest to record in the enumeration other statistics, beyond the edge number.
We will present solutions for some bivariate problems, obtained in collaboration with Andrew Elvey Price (Tours).

Mingkun Liu : Length spectra of random metric maps: a Teichmüller theory approach (slides)

In this talk, I will first discuss short closed geodesics on a random hyperbolic surface of large genus, and we will see that the lengths of these geodesics are distributed in exactly the same way as those of the short cycles in a big random map (following the work of Mirzakhani–Petri and Janson–Louf). Next, I will present a joint work with Simon Barazer and Alessandro Giacchetto, where we study random maps of large genus with a Teichmüller theory approach.

Armand Riera : Excursion theory for Markov processes indexed by Lévy Trees (slides, source )

This talk deals with Markov processes indexed by Lévy trees. This class of processes plays a fundamental role in probability theory due to their relationships with superprocesses, their appearance in various limit theorems, and their connections with growth-fragmentation processes. Moreover, they enable the construction of two-dimensional random geometry models. In particular, Brownian motion indexed by the Brownian tree has been used as a building block to construct various models of Brownian surfaces, such as the Brownian map.
Our goal is to present a new excursion theory for this family of processes by adapting ideas from analogous discrete models. This theory provides a comprehensive framework for understanding the evolution of these processes between visits to a reference point. It naturally extends the classical excursion theory of Markov processes indexed by the real half-line and recover previous results obtained by Abraham and Le Gall in the special case of Brownian motion indexed by the Brownian tree.
Finally, time permitting, we will discuss applications to the scaling limits of various discrete models.
This presentation will be entirely self-contained and will not require any prior specialized knowledge. The results presented are part of joint work with Alejandro Rosales-Ortiz.

Meltem Ünel : A view on height coupled trees (slides)

We shall first give an overview of the existing results for the model of planar rooted random trees whose distribution is even for fixed height h and size N and whose height dependence is power-like h(T)^α and is of exponential form exp(-μ h). We shall then focus on the case one-sided trees, rooted planar trees whose maximal path is the leftmost (or the rightmost) one, in the existence of exponential weights. Defining the total weight for such trees of fixed size to be Z_N^(μ), we determine its asymptotic behavior for large N, for arbitrary real values of μ. Based on this we evaluate the local limit of the corresponding probability measures and find a transition at μ= - log 2 from a single spine phase to a multi-spine phase, meaning that the limit in the uniform case μ=0 is multi-spine. These results are obtained in a series of papers in collaboration with Bergfinnur Durhuus.
Time permitting, we will conclude with a glimpse on certain results from an ongoing work with L. Addario-Berry, B. Corsini and N. Maitra, concerning a generalization of the existing results.

Baptiste Louf : Counting with random walks (slides)

We are interested in an enumerative problem, namely counting geometric objects called combinatorial maps, which can be parametrized by two numbers: their size, and a topological parameter called the genus. We are interested in an asymptotic estimation of the number of these objects when both the size and the genus go to infinity.
While enumeration in one parameter is a very well studied topic with many powerful tools available, this problem is a case of bivariate enumeration, is a rather new topic with very few results known at the moment.
Our method consists in studying a recurrence formula for these maps and modeling it by a random walk, forgetting completely about the combinatorics of the model.
This is a work in progress with Andrew Elvey-Price, Wenjie Fang and Michael Wallner.

Vendredi 4/10

Michael Drmota : The method of moments revisited with applications to planar maps (slides)

The classical method of moments is used to prove limiting distributions by showing that properly centralized and/or scaled moments of a random variable converge to the corresponding moments of the limit. However, it is not always easy to obtain precise asymptotics for centralized moments - for example for proving a central limit theorem - due to "heavy cancellations". The main goal of this talk is to show some applications to random planar maps of a method of moments by Gao and Wormald that proves a central limit theorem without centralized moments.
This is joint work with Eva-Maria Hainzl and Nick Wormald.

Alice Contat : Parking on Cayley trees & Frozen Erdös-Rényi (slides)

Consider a uniform rooted Cayley tree T_n with n vertices and let m cars arrive sequentially, independently, and uniformly on its vertices. Each car tries to park on its arrival node, and if the spot is already occupied, it drives towards the root of the tree and parks as soon as possible. Using combinatorial enumeration, Lackner & Panholzer established a phase transition for this process when m is approximately n/2 . We couple this model with a variation of the classical Erdös–Rényi random graph process. This enables us to describe completely the phase transition for the size of the components of parked cars using a modification of the standard multiplicative coalescent which we named the frozen multiplicative coalescent.
The talk is based on joint work with Nicolas Curien.

Andrew Elvey Price : Classification of D-finite walks in the quarter plane via elliptic functions (slides)

Given a set of small steps, we consider the three variable generating function counting walks in the quarter plane using these steps. Since the seminal paper by Bousquet-Mélou and Mishna, the problem of characterising the generating function into the hierarchy Algebraic ⊂ D-finite ⊂ D-algebraic has received a lot of attention. For unweighted walks this characterisation is complete, however the existing proof of D-finiteness does not generalise to weighted walks. In this talk I will describe our new proof that the generating function is D-finite in each variable if and only if the group of the walk is finite. This result applies to any weighted model and is based on the elliptic function method.
This is joint work with Thomas Dreyfus and Kilian Raschel.

Enrica Duchi : From catalytic to algebraic decomposition, bijectively (slides)

A celebrated result of Bousquet-Mélou and Jehanne states that under reasonable combinatorial hypotheses the solutions of polynomial equations with one catalytic variable are algebraic series. We give a combinatorial derivation of this result in the case of order one catalytic equations (those involving only one univariate unkown series), in the form of a recipe to derive systematically an algebraic decomposition or a bijection with a simply generated family of trees from an order one catalytic decomposition.
Joint work with Gilles Schaeffer

Quentin Berger : FK-percolation and Recursions on Galton-Watson Trees (blackboard presentation)

Some statistical mechanics models on trees may sometimes reduce to the study of some "simple" tree recursion; this is for instance the case for the FK-percolation model. It turns out that when the recursion is concave, we can compare this tree recursion to the one verified by (possibly non-linear) resistive networks.
I will present a recent work with Irene Ayuso Ventura (Créteil), in which we obtain precise estimates on the asymptotic behaviour of non-linear conductances of Galton-Watson tree, also deriving some information on the FK-percolation model on random trees.

Personnes connectées : 2

Vie privée