|
|
|
|
Bienvenue ! Nous organisons deux journées de conférences les 3 et 4 octobre 2024 en combinatoire et probabilités. Ces journées s'inscrivent dans le cadre de l'axe 3 (Physique mathématique, Physique Statistique, Combinatoire) de la fédération de recherche Math-STIC de l'Université Sorbonne Paris Nord, qui associe les laboratoires de mathématiques (LAGA), d'informatique (LIPN) et de traitement et transmission de l'information (L2TI). Les exposés auront lieu dans l'amphi Euler de l'Institut Galilée. Des repas (buffets) seront proposés le midi. L'inscription est gratuite mais obligatoire pour faciliter l'organisation. Les inscriptions sont désormais closes. Liste des orateurs
Programme
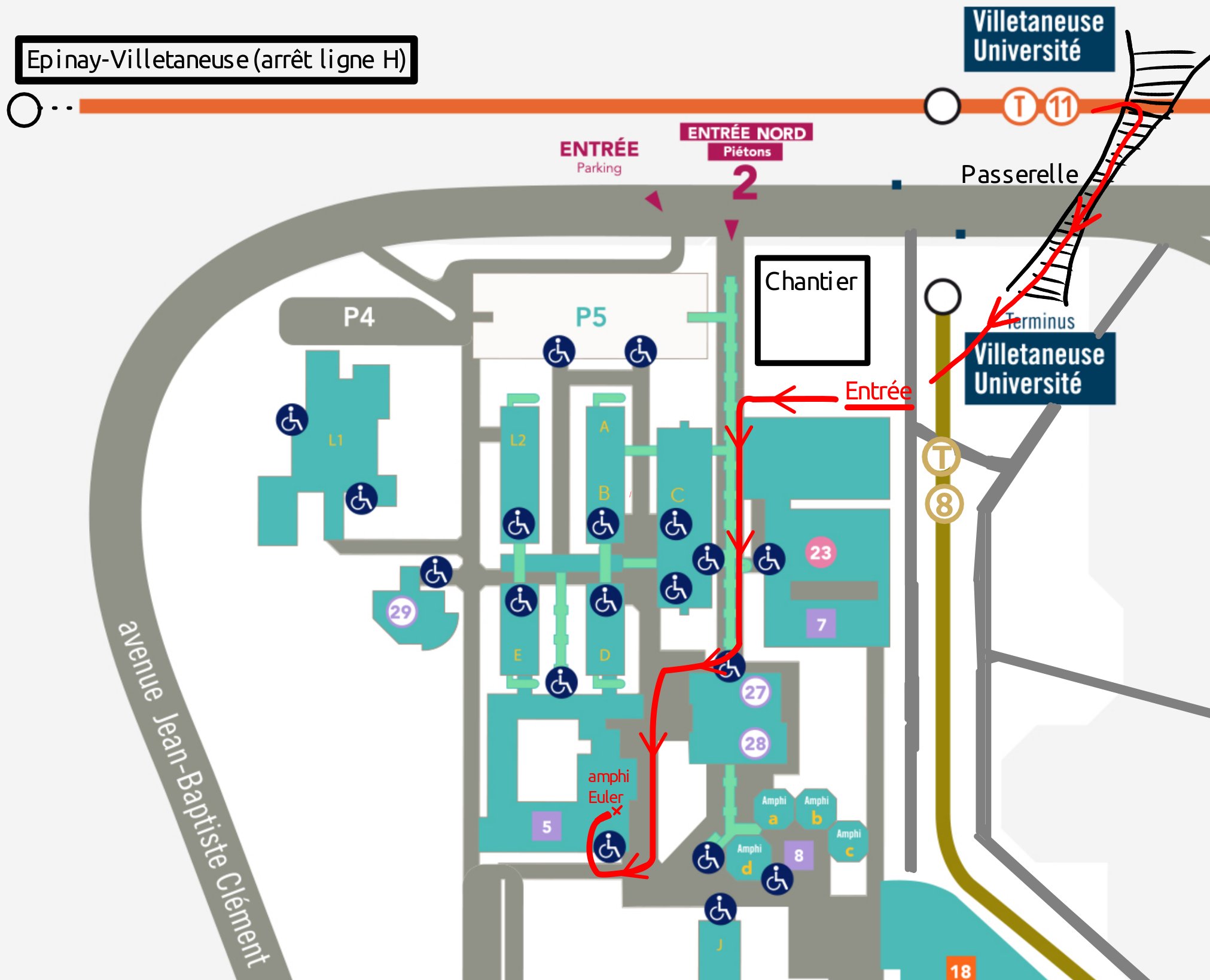
Jeudi 3/10Mireille Bousquet-Mélou : Combinatorics of 3-coloured quadrangulations (slides) This talk deals with the enumeration of (planar) maps equipped with a proper 3-colouring of their vertices. The case of triangulations is well-understood, with an algebraic generating function and bijective solutions. The case of general planar maps is still algebraic, but the combinatorial explanations for that are missing. We will focus on quadrangulations, for which algebraicity is lost. Mingkun Liu : Length spectra of random metric maps: a Teichmüller theory approach (slides) In this talk, I will first discuss short closed geodesics on a random hyperbolic surface of large genus, and we will see that the lengths of these geodesics are distributed in exactly the same way as those of the short cycles in a big random map (following the work of Mirzakhani–Petri and Janson–Louf). Next, I will present a joint work with Simon Barazer and Alessandro Giacchetto, where we study random maps of large genus with a Teichmüller theory approach. Armand Riera : Excursion theory for Markov processes indexed by Lévy Trees (slides, source) This talk deals with Markov processes indexed by Lévy trees. This class of processes plays a fundamental role in probability theory due to their relationships with superprocesses, their appearance in various limit theorems, and their connections with growth-fragmentation processes. Moreover, they enable the construction of two-dimensional random geometry models. In particular, Brownian motion indexed by the Brownian tree has been used as a building block to construct various models of Brownian surfaces, such as the Brownian map. Meltem Ünel : A view on height coupled trees (slides) We shall first give an overview of the existing results for the model of planar rooted random trees whose distribution is even for fixed height h and size N and whose height dependence is power-like h(T)α and is of exponential form exp(-μ h). We shall then focus on the case one-sided trees, rooted planar trees whose maximal path is the leftmost (or the rightmost) one, in the existence of exponential weights. Defining the total weight for such trees of fixed size to be ZN(μ), we determine its asymptotic behavior for large N, for arbitrary real values of μ. Based on this we evaluate the local limit of the corresponding probability measures and find a transition at μ= - log 2 from a single spine phase to a multi-spine phase, meaning that the limit in the uniform case μ=0 is multi-spine. These results are obtained in a series of papers in collaboration with Bergfinnur Durhuus. Baptiste Louf : Counting with random walks (slides) We are interested in an enumerative problem, namely counting geometric objects called combinatorial maps, which can be parametrized by two numbers: their size, and a topological parameter called the genus. We are interested in an asymptotic estimation of the number of these objects when both the size and the genus go to infinity. Vendredi 4/10Michael Drmota : The method of moments revisited with applications to planar maps (slides) The classical method of moments is used to prove limiting distributions by showing that properly centralized and/or scaled moments of a random variable converge to the corresponding moments of the limit. However, it is not always easy to obtain precise asymptotics for centralized moments - for example for proving a central limit theorem - due to "heavy cancellations". The main goal of this talk is to show some applications to random planar maps of a method of moments by Gao and Wormald that proves a central limit theorem without centralized moments. Alice Contat : Parking on Cayley trees & Frozen Erdös-Rényi (slides) Consider a uniform rooted Cayley tree T_n with n vertices and let m cars arrive sequentially, independently, and uniformly on its vertices. Each car tries to park on its arrival node, and if the spot is already occupied, it drives towards the root of the tree and parks as soon as possible. Using combinatorial enumeration, Lackner & Panholzer established a phase transition for this process when m is approximately n/2 . We couple this model with a variation of the classical Erdös–Rényi random graph process. This enables us to describe completely the phase transition for the size of the components of parked cars using a modification of the standard multiplicative coalescent which we named the frozen multiplicative coalescent. Andrew Elvey Price : Classification of D-finite walks in the quarter plane via elliptic functions (slides) Given a set of small steps, we consider the three variable generating function counting walks in the quarter plane using these steps. Since the seminal paper by Bousquet-Mélou and Mishna, the problem of characterising the generating function into the hierarchy Algebraic ⊂ D-finite ⊂ D-algebraic has received a lot of attention. For unweighted walks this characterisation is complete, however the existing proof of D-finiteness does not generalise to weighted walks. In this talk I will describe our new proof that the generating function is D-finite in each variable if and only if the group of the walk is finite. This result applies to any weighted model and is based on the elliptic function method. Enrica Duchi : From catalytic to algebraic decomposition, bijectively (slides) A celebrated result of Bousquet-Mélou and Jehanne states that under reasonable combinatorial hypotheses the solutions of polynomial equations with one catalytic variable are algebraic series. We give a combinatorial derivation of this result in the case of order one catalytic equations (those involving only one univariate unkown series), in the form of a recipe to derive systematically an algebraic decomposition or a bijection with a simply generated family of trees from an order one catalytic decomposition. Quentin Berger : FK-percolation and Recursions on Galton-Watson Trees (blackboard presentation) Some statistical mechanics models on trees may sometimes reduce to the study of some "simple" tree recursion; this is for instance the case for the FK-percolation model. It turns out that when the recursion is concave, we can compare this tree recursion to the one verified by (possibly non-linear) resistive networks. Plan d'accès L'accès recommandé se fait via l'arrêt "Villetaneuse Université" du tramway-express T11 (connection ligne B à "Le Bourget", ligne C à "Epinay-sur-Seine", ligne D à "Pierrefitte-Stains", ligne H (gare du Nord) à "Epinay-Villetaneuse") ou du tramway T8 NB. L'amphithéâtre Euler et la salle des buffets se trouvent au rez-de-chaussée Organisateurs
|
|||||||||||||||||||||||||||||||||||||